BTS CIRA - TP de physique première année
MESURE DE DEBIT AU VENTURI (suite)
|
page 4/4 Théorie du Venturi : 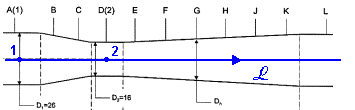
L’écoulement de l’eau se fait à température constante donc la masse volumique
de l’eau v1 S1 = v2 S2 Quand la section diminue, la vitesse d’écoulement augmente ( z représente la côte d’un point ; ici, z1 = z2 donc : Puisque S1 > S2 alors v1 < v2 donc : Lorsque la pression dynamique On remplace dans {E1} les vitesses en fonction du débit-volume:
ce qui donne : Détermination de la différence de pression p1 - p2 :
Finalement, il est possible d’écrire la relation
En remplaçant dans {E2} : Ce qui donne la relation finale du débit : En posant : Les diamètres des sections S1 et S2 sont respectivement égaux à 26,0 mm et 16,0 mm. La valeur calculée de C est : C = 9,62.10 - 4 (uSI) |
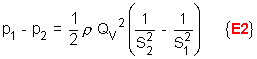
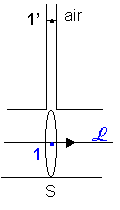
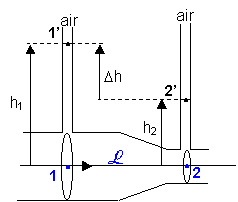
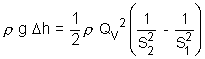
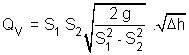
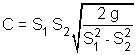 , (coefficient lié
aux dimensions du Venturi)
, (coefficient lié
aux dimensions du Venturi)