Donné en décembre 1998.
EXERCICE :
Une conduite ( dite gravitaire ) amène l' eau ( incompressible, de masse volumique r ) d' un barrage de grande capacité vers la turbine ( non représentée ) d' une centrale hydroélectrique. La conduite cylindrique, de diamètre constant D = 30 cm et de longueur L = 200 m, se termine horizontalement, son axe étant situé à la côte z = 0 ; La surface libre de l' eau, de niveau pratiquement constant dans le barrage se trouve à H = 160 m. Le départ de la conduite est à H 0 = 140 m. ( FIGURE 1 )
On négligera tout frottement et on donne :
- la pression atmosphérique P 0 = 1,0.10 5 Pa ( constante ).
- r = 1000 kg.m - 3 ( température uniforme ) ; g = 9,81 m.s - 2.
1) a) En appliquant le théorème de Bernoulli entre les points A et B, exprimer la vitesse de sortie v B en fonction de g et H. Calculer v B.
b) Vérifier que le débit-volume vaut environ 4 m 3.s - 1 ; Calculer le débit-masse de l' écoulement .
2) Soit un point C, de côte z, appartenant à la conduite ( avec 0 < z < H 0 ).
En appliquant le théorème de Bernoulli entre les points C et B, exprimer la pression p C en fonction de z Vérifier que p C diminue linéairement lorsque z augmente.
3) On rappelle que le phénomène de cavitation se produit lorsque la pression calculée en un point est inférieure ou égale à la pression de vapeur saturante de l' eau : p £ p VS.
Il y aura donc cavitation dans la conduite si p C £ p VS ; Déterminer la côte z des points pour lesquels se produit le phénomène de cavitation dans la conduite ( pour le calcul, on fera l' approximation suivante : p VS << P 0 ).
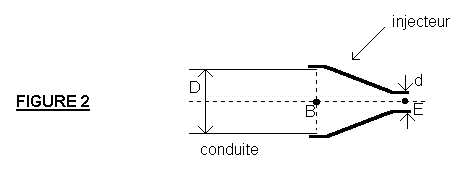
4) Pour remédier à ce problème ( pouvant provoquer la rupture de la conduite ), on visse à l' extrémité B une tubulure de section décroissante ( nommée injecteur ) de diamètre de sortie d < D et d' axe horizontal. ( FIGURE 2 ). On veut montrer que la conduite dans ce cas ne peut plus être en cavitation.
L' injecteur a un diamètre de sortie d = 15 cm.
a) Calculer la vitesse de sortie de l' eau au point E. En déduire le nouveau débit-volume de l' écoulement.
b) Calculer la vitesse en un point C de la conduite.
c) La condition de non -cavitation dans la conduite s' écrivant p C > p VS , montrer que cette condition est réalisée pour tout point C de côte z appartenant à la conduite ( avec 0 < z < H 0 ).
|
|