EXERCICE : PROPRIETES D’ UN FLUIDE. Parties A , B et C indépendantes.
A) Une large cuve de stockage, parallélépipédique
de hauteur H = 4 m contient un acide de masse volumique 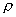 1
= 1200 kg.m-3 ainsi qu’ un autre liquide (fluide X), moins
dense que l’ acide, de masse volumique
1
= 1200 kg.m-3 ainsi qu’ un autre liquide (fluide X), moins
dense que l’ acide, de masse volumique 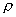 = 600 kg.m-3 et non miscible à l’ acide.
= 600 kg.m-3 et non miscible à l’ acide.
Au dessus de ce liquide se trouve un gaz à la pression p0.
Une prise de pression placée dans la partie inférieure de la cuve est reliée
à un tube en U au moyen d’ un fin tuyau souple. Le tube, ouvert à l’ air,
contient du mercure Hg ( 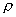 Hg
= 13600 kg.m-3).
Hg
= 13600 kg.m-3).
Le niveau S est au niveau du fond de la cuve ( en A) et la dénivellation du mercure est h = 30,0 cm.
1) Exprimer la différence de pression pA – p0 en
fonction notamment de H, 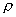 et
et 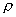 1.
1.
2) Que peut-on dire de la pression aux points A et S ? Exprimer pS en fonction notamment de h.
3) En déduire alors l’ expression de p0 ; Calculer p0. Quelle est la pression relative du gaz ?
4) Quelle est la dénivellation du mercure h’ si la branche droite du manomètre est reliée à la partie de la cuve qui contient le gaz (le gaz remplissant la branche du manomètre sans variation notable de volume dans la cuve) ?
Donnée : p Atm = 1,000.10 5 Pa ; prendre g = 10 m.s -2
 |
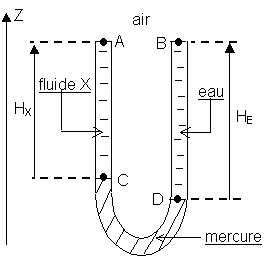
B) Afin de mesurer précisément la masse volumique du fluide X,
on remplit un manomètre en U (branches ouvertes à l’ air) avec 3 fluides
en procédant de la manière suivante : Dans le fond du tube, on place
du mercure puis on remplit simultanément la branche de droite avec de
l’ eau, la branche de gauche avec le fluide de masse volumique  X.
Le tube est rempli à ras bord. Les 3 fluides sont au repos dans le seul
champ de pesanteur.
X.
Le tube est rempli à ras bord. Les 3 fluides sont au repos dans le seul
champ de pesanteur.
On néglige tout phénomène de capillarité dans cette question.
Données :
masse volumique de l’ eau : 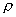 E
= 1000 kg.m-3
E
= 1000 kg.m-3
masse volumique du mercure : 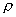 Hg
= 13600 kg.m-3
Hg
= 13600 kg.m-3
On mesure la hauteur d’ eau : HE = 1,000 m.
On mesure la hauteur de fluide X : HX = 0,970 m.
1) Ecrire pour chacun des 3 fluides la relation de la statique des fluides.
2) A partir des 3 relations précédentes, établir l’ expression de la masse
volumique 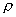 X
du fluide X en fonction de HE, HX,
X
du fluide X en fonction de HE, HX, 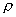 E
et
E
et 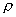 Hg.
Hg.
3) Calculer 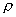 X.
Comparer avec la valeur partie A en calculant l’ écart relatif avec
X.
Comparer avec la valeur partie A en calculant l’ écart relatif avec 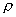 .
.
C) Pour déterminer la tension superficielle AX du fluide X , on le place successivement dans des tubes capillaires de rayon r différent et on mesure la hauteur h correspondant au phénomène de capillarité.
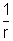 ) suivant :
) suivant :
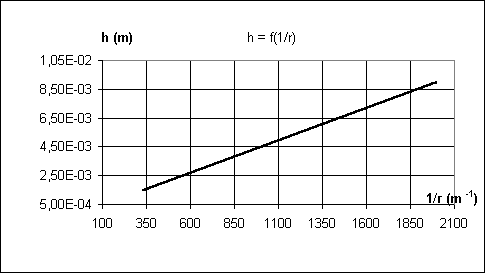
1) Déterminer l’ équation de la droite h = f( 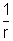 ) à partir du graphique. Justifier qu’ il s’ agit d’ un liquide mouillant
. Faire le schéma de l’ expérience avec un tube.
) à partir du graphique. Justifier qu’ il s’ agit d’ un liquide mouillant
. Faire le schéma de l’ expérience avec un tube.
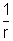 ), déterminer la tension superficielle AX du fluide X
en prenant :
), déterminer la tension superficielle AX du fluide X
en prenant :
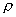 = 600 kg.m-3 ; q
= 60° ; g = 10 m.s –2.
= 600 kg.m-3 ; q
= 60° ; g = 10 m.s –2.
|
|