EXERCICE :
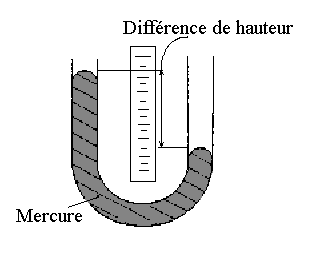
1) La sensibilité d’ un baromètre à mercure ( voir figure 1
ci-dessous) est donnée par la formule :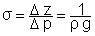 
|
figure 1
|
 |
Calculer la sensibilité de ce baromètre dans le cas du mercure. L’ exprimer en mm par torr (133,3 Pa).
On prendra : r = 13 600 kg.m – 3 ; g = 9,81 m.s – 2
2) Huyghens a mis au point un baromètre dont on va calculer la sensibilité s ‘. Le baromètre, représenté figure 2, comporte une cuve à mercure. Soit S l’ aire de la surface libre du mercure dans cette cuve.
Un tube barométrique comporte un petit réservoir (R) de section s 1 et est surmonté d’ un tube plus fin (T) de section s 2. Le mercure monte jusqu’ à une certaine hauteur vers le milieu de (R) ; il est surmonté par de la glycérine (masse volumique r 1 ) dont la surface libre est à un certain niveau vers le milieu de (T).
L’ espace au-dessus de la glycérine est considéré comme vide.
 |
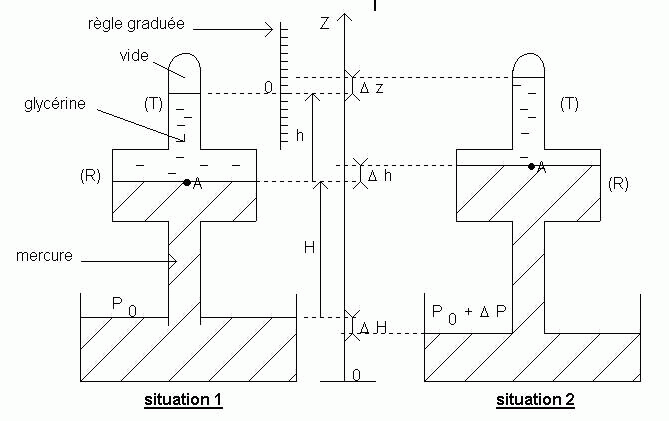a) L' appareil est d' abord équilibré à la pression atmosphérique locale P 0 ; la glycérine affleure à la graduation 0 d' une règle. ( cf. situation 1 ).
Exprimer P0 en fonction de r, r 1 , g , H et h.
b) La pression atmosphérique augmente de DP : le niveau de la glycérine monte de Dz dans le tube (T) . ( cf. situation 2 ).
Exprimer DP en fonction de r, r 1 , g, DH, Dh et Dz. ( On utilisera la relation obtenue à la question précédente).
On démontrera que : DP = ( r – r1 ) g Dh + r g DH + r1 g Dz.
c) Exprimer maintenant DP en fonction de r, r 1 , g , Dz, S, s 1 et s 2.
d) Calculer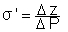 
. L’ exprimer en mm par torr (133,3 Pa ).
Données : r 1 = 1050 kg.m –3 ; S = 50 cm 2 ; s 1 = 5 cm 2 ; s 2 = 0,2 cm 2
e) Comparer s et s ‘. Conclusion.
|
|
|
|
|
