EXERCICE :             Donné en mars 1999

A) Le mur extérieur d’ une pièce d’ habitation fait 2,80 m de hauteur et 4,20 m de long. Il a une épaisseur e ₁ = 24 cm et est constitué de briques dont la conductivité thermique est  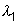:  = 0,836 W.m ^-1.K ^-1.

Une fenêtre de grand vitrage de 1,50 m de large et de 1,80 m de haut est placée dans le mur. Les vitres d’ épaisseur e₂ = 5 mm sont constituées d’ un verre ayant une conductivité thermique 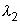 = 0,778  W.m ^-1.K ^-1. ( L’ influence des boiseries est négligeable ).

On admet que le coefficient d’ échange thermique ( ou convectif ) avec l’ air vaut côté intérieur et côté extérieur h = h _ci = h _ce = 2,62 W.m ^-2.K ^-1.

Les déperditions par les autres murs de la pièces sont négligeables.

1) Calculer la surface des vitres, celle du mur et celle des briques.

2) Calculer la résistance thermique totale des vitres et la résistance thermique totale pour les briques.

3) Calculer le flux de chaleur total échangé à travers le mur si l’ on veut maintenir la température à l’ intérieur de la pièce d’ habitation à 20 °C sachant que la température extérieure est de - 5 °C.

B) Pour réaliser une isolation thermique, on pense utiliser un matériau de conductivité thermiqu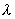e . Pour déterminer cette conductivité thermique, on effectue en laboratoire l’ expérience suivante :

On place une plaque de 20 mm d’ épaisseur de faces A et B pratiquement infinies (très grandes dimensions devant celle du matériau utilisé pour l' expérience) entre deux parois, l’ une chaude (contre A), l’ autre froide ( contre B ) constituées du même matériau dont la conductivité est 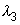 = 0,267 W.m ^-1.K ^-1.

On mesure la température T₁ = 68 °C dans la paroi chaude à 2 mm de la face A et T₂ = 14 °C dans la paroi froide également à 2 mm de la face B. Par ailleurs on mesure également la température de la face A : T_A = 65 °C.

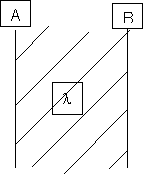
Les calculs seront effectués pour 1 m ² de surface plane.

1) Calculer le flux thermique 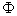 échangé dans la plaque chaude.

2) Calculer la résistance thermique totale de l’ ensemble ainsi réalisé.

3) En déduire alors la conductivité thermique 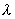 du matériau.

C) On recouvre les briques du mur de l’ habitation précédente avec des plaques de 15 mm d’ un matériau isolant de conductivité thermique 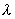 = 0,167 W.m ^-1.K ^-1.

Calculer le nouveau flux à travers les briques ainsi que le gain d’ énergie réalisé.