Donné en novembre 2001.

EXERCICE  :

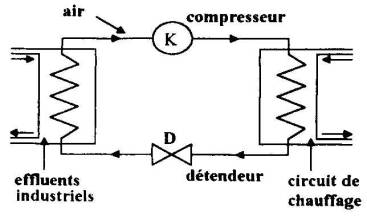
On s'intéresse à une pompe à chaleur qui participe au chauffage de locaux, en prélevant de la chaleur aux effluents liquides à température élevée d'une installation industrielle, avant leur rejet dans une rivière qui recevra des effluents à température plus faible.

L'installation représentée ci-dessous comporte un compresseur, un détendeur et deux serpentins qui sont le siège des échanges thermiques, avec les effluents d'une part, et avec l'eau d'un circuit de chauffage d'autre part.

Le fluide frigorigène est de l'air, assimilé à un gaz parfait

On étudie les transformations réversibles de 1 kg d'air qui décrit le cycle suivant :

1-2 :    dans le compresseur :         compression isentropique, la pression passant de p₁ = 10⁵ Pa à p₂ = 2.10⁵ Pa et la température passant de T₁ = 310 K à T₂.

2-3 :   dans le serpentin au contact du circuit de chauffage ( V₃ < V₂ ) :         refroidissement isobare, la température passant de T₂ à T₃ = 330 K

3-4 :    dans le détendeur :              détente isentropique, la pression passant de P₃ = P₂ à P₄ = P₁, la température passant de T₃ à T₄.

4-1 :    dans un serpentin plongé dans les effluents industriels :           échauffement isobare jusqu'à la température T₁.

Données :

·        capacité thermique massique de l'air à pression constante : c_p = 1000 J.kg ^-1. K ^-1

·        exposant adiabatique :       g = 1,40

1) Représenter l'allure du cycle décrit par l'air sur un diagramme de Clapeyron (p, V) puis dans le diagramme entropique (T,S) en fléchant le sens des transformations. Que représente l’ aire du cycle dans chaque diagramme ?

2) Montrer que T₂ # 378 K et T₄ # 271 K

3) Calculer les quantités de chaleur échangées par, une masse de 1 kg d'air au cours de chacune des 4 transformations.

4) Enoncer le premier principe de la thermodynamique pour un cycle. En déduire le travail W reçu par la masse de 1 kilogramme d'air au cours du cycle.

5) A l’ aide du deuxième principe de la thermodynamique, calculer pour les 2 transformations isobares du cycle les variations d' entropie du gaz parfait et vérifier que l' on a : ( DS ) _cycle = 0.

6) On désigne par (e_th)_r l'efficacité thermique réelle de la pompe à chaleur, c’ est à dire le rapport de la quantité de chaleur reçue par la source chaude et du travail reçu par l'air, au cours d'un cycle. Calculer (e_th)_r.

7) Calculer l’ efficacité thermique e_th de cette machine qui fonctionnerait suivant un cycle de Carnot entre les températures T₁= T_C et T₃ = T_F. En déduire le rendement de l’ installation défini par :