- Pertes de charge et régime d' écoulement

- Théorème de Bernoulli généralisé : à connaître

EXERCICE 1 :

Une pompe assurant un débit Q v dans un circuit où la perte de charge est Dp, développe une puissance P = Q v . Dp.

1) Vérifier que le produit Q v . Dp a bien les dimensions d' une puissance.

2) On considère un tuyau horizontal dans lequel circule une huile dont la masse volumique est r = 800 kg.m ^{- 3} et la viscosité h = 0,10 Pa.s à la température de l' expérience. La conduite a pour longueur L = 10 km et pour diamètre 10 cm. On souhaite assurer un débit de 20 m ³.h ^{- 1}.

a) Vérifier que dans ces conditions, l' écoulement est laminaire ( Calculer le nombre de Reynolds ).

b) Quelle doit être la puissance de la pompe ?

EXERCICE 2 :

Pour un écoulement régi par la loi de Poiseuille, la perte de charge par unité de longueur s' écrit :

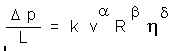où v est la vitesse moyenne d' écoulement et k un facteur numérique sans

dimension. Déterminer par analyse dimensionnelle les coefficients a, b et d.

EXERCICE 3 :

Déterminer le régime d' écoulement dans une canalisation de 30 cm de diamètre :

*Pour de l' eau circulant à la vitesse moyenne de 10,5 m/s et de viscosité cinématique 1.10 ^{- 6} m²/ s

*pour du fuel lourd à 50 °C circulant à la même vitesse ( viscosité cinématique 110.10 ^{- 6} m² / s ).

EXERCICE 4 :

1) Pour déterminer les pertes de charge par mètre de conduite droite, on installe sur une canalisation deux prises de pression pratiquées dans la paroi à une distance de 5 m l' une de l' autre. La D p mesurée est 5000 Pa.

a) Calculer la chute de pression exprimée en Pa.m ^-1 .

b) Calculer la perte de charge J en mètre de liquide ( eau ) puis la perte de charge j en mètre d' eau par mètre de canalisation droite.

2) On s' intéresse à la perte de charge créée par un coude à angle droit de la conduite. En plaçant deux prises de pression située à 50 cm avant le coude et 50 cm après le coude, on mesure D p = 1500 Pa.

A quelle longueur L _éq de conduite droite ce coude est il équivalent pour les pertes de charge ?

EXERCICE 5 :

Un fluide de masse volumique r = 890 kg.m ^{- 3} et de viscosité moyenne h = 0,275 Pa.s s' écoule dans une conduite horizontale de diamètre d = 150 mm à partir d' un réservoir de très grande section ouvert à l' air libre.

Sur la partie horizontale de ce tube sont installés deux manomètres distants de L = 120 m ; On relève les pressions relatives suivantes : P₂ = 1,1 bar ; P₃ = 0,45 bar ( 1 bar = 10 ⁵ Pa ).

1) a) La vitesse moyenne d' écoulement dans le tube étant v = 1,40 m.s ^{- 1}, calculer le nombre de Reynolds et vérifier que l' écoulement est laminaire.

b) Calculer alors la valeur du coefficient de pertes de charge l.( g = 10 m.s ^{- 2} ).

2) Calculer la puissance dissipée entre 2 et 3 à cause des pertes de charge.

3) En négligeant la perte de charge singulière au point A ( rétrécissement ), calculer la hauteur H de liquide dans le réservoir.

EXERCICE 6 :

Le réservoir ci-contre ( de très grande section ) permet d' alimenter en eau une installation industrielle ( non représentée ).L' eau est transportée par une canalisation en fonte de diamètre D = 100 mm. 1) En négligeant toute perte de charge, calculer la vitesse de sortie en B de l' eau si PA - PB = Patm.

2) Dans cette question, on tient compte des pertes de charge.

Calculer le nombre de Reynolds R _e en prenant comme vitesse moyenne d' écoulement la vitesse précédemment calculée ( v _B = 14 m / s ). Vérifier que le régime est turbulent.

3) a) En utilisant l' abaque de Colebrook fourni (consulter le document distribué en cours ), calculer le coefficient de frottement ou de pertes de charge l dans la canalisation sachant que la rugosité moyenne de la canalisation est e = 0,2 mm.

b) Exprimer alors les pertes de charges régulières en fonction de v ²_B ( nouvelle vitesse d' écoulement ) si la longueur droite de la canalisation est L = 107 m.

4) Pour calculer les pertes de charges singulières ( coude, vanne ... ), on donne la valeur numérique d' un coefficient K de perte de charge caractérisant chaque singularité.

- entrée de la canalisation : K ₁ = 0,5.

- coude à 90 ° : K ₂ = 0,3.

- robinet vanne : K ₃ = 0,15.

- sortie de la canalisation : K ₄ = 1.

Exprimer alors les pertes de charges singulières en fonction de v ²_B .

5) Ecrire de nouveau le théorème de Bernoulli ente A et B puis calculer la nouvelle vitesse d' écoulement v _B.

6) Recalculer alors le nombre de Reynolds. La valeur de l est - elle modifiée ?

EXERCICE 7 :

Une pompe placée en aspiration prélève à raison de 15 m ³.h ^-1 par l' intermédiaire d' une conduite de 160 mm de diamètre de l' eau à 20 °C contenue dans un réservoir à niveau maintenu constant. La perte de charge en amont de la pompe est de 0,5 m d' eau.

Sachant que la pression de vapeur saturante de l' eau est à 20 °C de 2500 Pa, calculer la hauteur maximale h à laquelle on peut placer la pompe pour éviter qu' elle cavite.

P_atm = 1,013.10 5 Pa. Le réservoir est de large section.

Fiches de révisions

Accueil