|
Buts : - Recherche de (des) la loi(s) de variation de la pression de vapeur saturante de l'eau en fonction de la température T dans un domaine de température restreint.
- Exploitation graphique et utilisation de la relation de Clapeyron.
A) Introduction théorique :
La masse volumique de l'eau liquide est 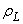 = 1000 kg/m 3 supposée constante. Sa masse molaire moléculaire est M = 18 g/mol. = 1000 kg/m 3 supposée constante. Sa masse molaire moléculaire est M = 18 g/mol.
Le tableau ci-dessous donne la pression de vapeur saturante P (en bar) de l'eau en fonction de la température T (en K). (1bar = 105 Pa).
T |
323 |
328 |
333 |
338 |
343 |
348 |
353 |
358 |
363 |
368 |
373 |
P |
0,123 |
0,157 |
0,199 |
0,250 |
0,312 |
0,386 |
0,474 |
0,578 |
0,701 |
0,845 |
1,013 |
On admettra, en première approximation, que l'équation d'état des gaz parfaits s'applique à la vapeur monophasée et à la vapeur saturante sèche.
La constante des gaz parfaits est R = 8,314 J.K -1.mol -1.
Changement d'état :
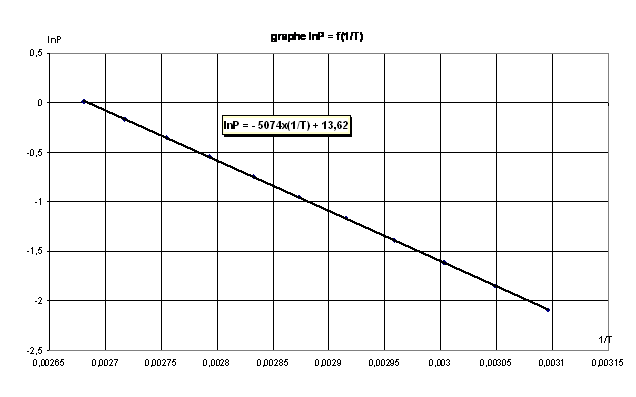
1) Représenter graphiquement : P en fonction de T puis ln P en fonction de 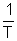 . .
2) En déduire la valeur des coefficients A et B de la loi 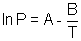 (on démontrera la relation théorique utilisée avant de faire l'application numérique). (on démontrera la relation théorique utilisée avant de faire l'application numérique).
Proposition de solution :
 |
Le graphe représenté ci-dessus montre que la pression P de changement d'état liq-vap est une fonction croissante de la température de changement d'état ;
Les domaines L et V doivent être indiqués (à T donnée, le domaine du liquide (phase condensée) est celui des pressions «élevées» ; La courbe de pression de vapeur saturante correspondant à l'équilibre liquide-vapeur.
Concernant le tracé du graphe ln P =f( 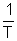 ), en ordonnée se trouve le logarithme népérien de la valeur de la pression de changement d'état exprimée en bar, et non pas de la pression elle même.(Il suffit de considérer que l'on calcule ), en ordonnée se trouve le logarithme népérien de la valeur de la pression de changement d'état exprimée en bar, et non pas de la pression elle même.(Il suffit de considérer que l'on calcule 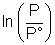 avec P° = 1 bar). avec P° = 1 bar).
La formule de Clapeyron relative à l'unité de masse de H2O pour la transition de phase liq-->vap s'écrit : 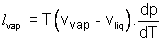 ; La valeur du volume massique de la vapeur s'écrit pour un gaz parfait : ; La valeur du volume massique de la vapeur s'écrit pour un gaz parfait : 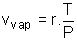 où r est la constante massique du gaz où r est la constante massique du gaz 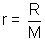 ; Le volume massique ; Le volume massique 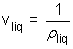 de H2O est constant or de H2O est constant or 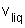 << << 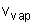 pour tous les couples de valeurs (p,T) donnés. (Les calculs le montrent). pour tous les couples de valeurs (p,T) donnés. (Les calculs le montrent).
Donc la formule de Clapeyron devient dans ces conditions 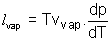 ce qui s'écrit : ce qui s'écrit : 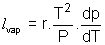 ; C'est une équation différentielle à variables séparables : ; C'est une équation différentielle à variables séparables : 
ce qui s'écrit aussi : 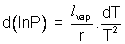 ; En passant à la forme intégrale, on obtient : ; En passant à la forme intégrale, on obtient : 
En faisant l'hypothèse que (l vap) varie peu avec la température sur l'intervalle de température [T0 ;T] : (l vap = cste), alors : 


Et finalement, en posant : 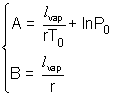 on peut écrire : on peut écrire : 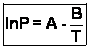 Cette loi est appelée loi de Rankine (Calendar). Cette loi est appelée loi de Rankine (Calendar).
Exploitation : La valeur de l'enthalpie massique de vaporisation de l'eau est obtenue, dans les conditions d'étude citées, grâce à l'expression de B (qui est l'opposé du coefficient directeur de la droite lnP = f( 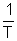 ) : ) : 
Le calcul de 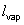 sur l'intervalle de température [50°C ; 100°C] donne, à partir de la valeur de B : sur l'intervalle de température [50°C ; 100°C] donne, à partir de la valeur de B : 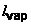 = 2 340 kJ/kg. = 2 340 kJ/kg.
Les tables de données thermodynamiques indiquent :
• à 50°C , 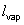 = 2 383 kJ/kg. = 2 383 kJ/kg.
• à 100 °C , 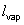 = 2 257 kJ/kg. = 2 257 kJ/kg.
Donc, en moyenne, entre ces 2 températures, 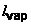 = 2 320 kJ/kg = 2 320 kJ/kg
L'écart relatif entre les valeurs tabulée et modélisée est inférieur à 1%, ce qui montre la validité du modèle de Rankine sur l'intervalle de température choisi. |
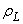 = 1000 kg/m 3 supposée constante. Sa masse molaire moléculaire est M = 18 g/mol.
= 1000 kg/m 3 supposée constante. Sa masse molaire moléculaire est M = 18 g/mol.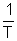 .
. 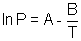 (on démontrera la relation théorique utilisée avant de faire l'application numérique).
(on démontrera la relation théorique utilisée avant de faire l'application numérique). 
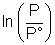 avec P° = 1 bar).
avec P° = 1 bar).
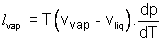 ; La valeur du volume massique de la vapeur s'écrit pour un gaz parfait :
; La valeur du volume massique de la vapeur s'écrit pour un gaz parfait : 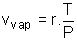 où r est la constante massique du gaz
où r est la constante massique du gaz 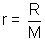 ; Le volume massique
; Le volume massique 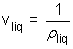 de H2O est constant or
de H2O est constant or 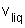 <<
<< 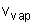 pour tous les couples de valeurs (p,T) donnés. (Les calculs le montrent).
pour tous les couples de valeurs (p,T) donnés. (Les calculs le montrent). 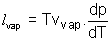 ce qui s'écrit :
ce qui s'écrit : 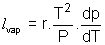 ; C'est une équation différentielle à variables séparables :
; C'est une équation différentielle à variables séparables : 
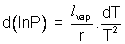 ; En passant à la forme intégrale, on obtient :
; En passant à la forme intégrale, on obtient : 



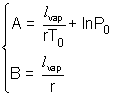 on peut écrire :
on peut écrire : 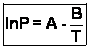 Cette loi est appelée loi de Rankine (Calendar).
Cette loi est appelée loi de Rankine (Calendar). 
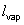 sur l'intervalle de température [50°C ; 100°C] donne, à partir de la valeur de B :
sur l'intervalle de température [50°C ; 100°C] donne, à partir de la valeur de B : 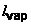 = 2 340 kJ/kg.
= 2 340 kJ/kg.