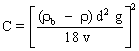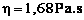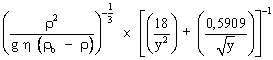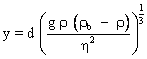BTS CIRA - TP de physique première année
MESURE DE LA VISCOSITE D'UN FLUIDE NEWTONIEN (suite)
|
page 3/3 Le nombre de Reynolds à prendre en compte est : Re =
Étude du graphe CX = f(Re ) (qui est en coordonnées logarithmiques) : Pour les nombres de Reynolds inférieurs à 0,60, la loi mathématique liant CX et Re est : 1) Pouvons-nous utiliser cette loi sachant que le nombre de Reynolds estimé (0,90) est voisin de 0,60 ?
Soit :
Ce qui donne :
Masse volumique de la bille : Application numérique :
Cette valeur présente un écart de 20 % par rapport à la valeur attendue ( 1,49 Pa.s ) ; La loi mathématique
En remplaçant Re par sa valeur calculée (0,85) , on trouve, à l'aide de la formule ci-dessus, un coefficent de traînée CX égal à 30,4 (qui correspond bien à la valeur attendue 30,0). En reprenant l'égalité {E} puis en élevant ses deux termes au carré, on obtient :
En remplaçant Re par son expression :
Soit encore :
Soit finalement :
On obtient une équation du second degré :
Avec La résolution de l'équation conduit à deux solutions dont une seule est positive et qui est la valeur recherchée :
L'écart relatif avec la valeur attendue n'est plus que de 13 % ; Cet écart non négligeable est du vraisemblablement à une modélisation imparfaite de la valeur de la vitesse v (effets de parois insuffisamment pris en compte) et nécessiterait d'utiliser une relation encore plus précise entre le coefficient de traînée et le nombre de Reynolds. |
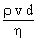
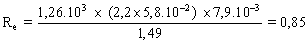
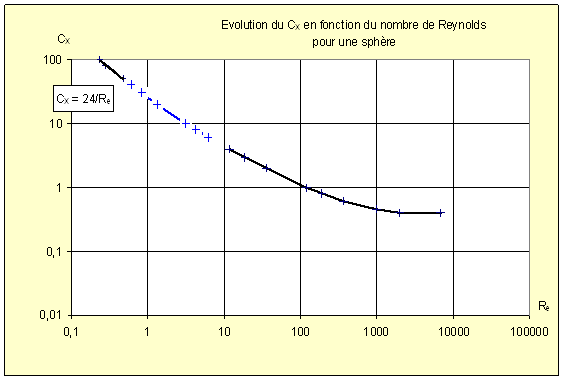
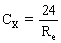
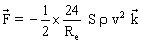
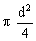 , on obtient :
, on obtient : 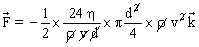
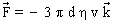 que l'on peut réécrire, puisque
que l'on peut réécrire, puisque 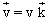 :
: 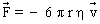 (ce qui constitue la loi de Stokes ).
(ce qui constitue la loi de Stokes ). 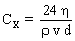 ;
; 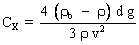
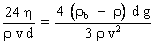
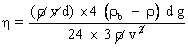

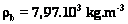
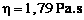
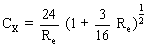

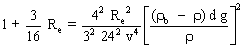
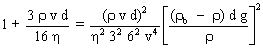
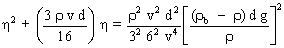
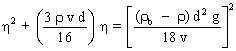
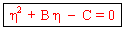
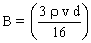 et
et