|
page 2/3
Etude simplifiée du mouvement de la bille :
Dans le référentiel du laboratoire (supposé galiléen), les forces extérieures qui s'appliquent sur la bille sont :
- le poids 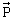 de la bille. (appliqué au centre de gravité G de la bille ; force verticale vers le bas). de la bille. (appliqué au centre de gravité G de la bille ; force verticale vers le bas).
- la poussée d'Archimède 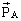 (appliquée au centre de poussée C confondu avec le centre de gravité G de la bille dans le cas étudié) : verticale vers le haut (appliquée au centre de poussée C confondu avec le centre de gravité G de la bille dans le cas étudié) : verticale vers le haut
- la force de frottement (force de traînée) exercée par le liquide : 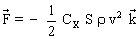 où où 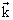 est un vecteur unitaire orienté dans le sens du mouvement de la bille (Force verticale vers le haut). est un vecteur unitaire orienté dans le sens du mouvement de la bille (Force verticale vers le haut).
S est le maître-couple de la bille (aire de la surface de la bille projetée dans un plan perpendiculaire à la direction du mouvement de la bille) et CX est le coefficient de traînée (CX dépend du nombre de Reynolds Re ).
le théorème du centre d'inertie (ou deuxième loi de Newton) appliquée à la bille s'écrit :
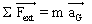 soit soit 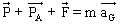
Lorsque la bille atteint sa vitesse de chute constante, le vecteur accélération de la bille est 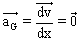 et : et :
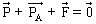
En projetant ces vecteurs sur l'axe vertical (OZ), on obtient : P - PA - F = 0 ou encore :
F = P - PA
Le poids de la bille s'exprime à partir de la masse volumique 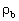 de la bille et de son volume : de la bille et de son volume : 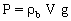 . .
La poussée d'Archimède PA est égale au poids du liquide déplacé par la bille : PA = mliq g or 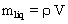 où où 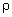 est la masse volumique de la glycérine donc est la masse volumique de la glycérine donc 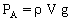 . .
On obtient :
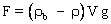
Le volume occupé par une bille de rayon r est 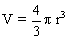 ou encore, puisque r = ou encore, puisque r = 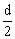 (d : diamètre de la bille), (d : diamètre de la bille), 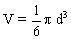 .On a alors : .On a alors :
F = 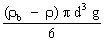 La norme de 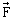 est est 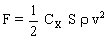 avec avec 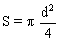 ; L'égalité précédente est réécrite : ; L'égalité précédente est réécrite :
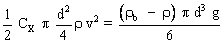
Soit :
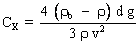 {E} {E}
Il est alors nécessaire de connaître soit la valeur de CX soit son expression ; CX dépend du nombre de Reynolds.
L'examen de la courbe CX = f(Re ) pour une sphère chutant dans un fluide visqueux montre la forte variation de CX pour les nombres de Reynolds inférieurs à 1000.
Un calcul permettant d'estimer la valeur de Re est donc nécessaire :
Dans l'expression du nombre de Reynolds, 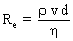 , v correspond à la vitesse moyenne relative du fluide par rapport au solide (dans le cas étudié : la bille supposée sphérique) , d est le diamètre intérieur du tube dans lequel s'écoule le fluide ou le diamètre de la bille en mouvement dans le fluide (dimension « caractéristique » du système étudié). , v correspond à la vitesse moyenne relative du fluide par rapport au solide (dans le cas étudié : la bille supposée sphérique) , d est le diamètre intérieur du tube dans lequel s'écoule le fluide ou le diamètre de la bille en mouvement dans le fluide (dimension « caractéristique » du système étudié).
La bille de diamètre d chutant dans un tube de diamètre D peu important, les effets de parois du tube (plus généralement l'étendue du milieu de chute) sont à prendre en compte, ces parois amenant une valeur minorée de la vitesse constante de chute v de la bille ; On introduit le coefficient 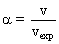 où vexp est la vitesse expérimentale de chute de la bille dans la glycérine (milieu limité par les parois du tube) et v la vitesse qu'aurait cette même bille dans la glycérine si le milieu était infini. C'est cette vitesse v à prendre en compte dans le calcul du nombre de Reynolds. où vexp est la vitesse expérimentale de chute de la bille dans la glycérine (milieu limité par les parois du tube) et v la vitesse qu'aurait cette même bille dans la glycérine si le milieu était infini. C'est cette vitesse v à prendre en compte dans le calcul du nombre de Reynolds.
Une expression tenant compte essentiellement du rapport (d/D), où D est le diamètre du tube, permet de calculer 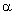 ; La relation utilisée est : ; La relation utilisée est : 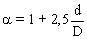
ce qui donne
v = 2,2 vexp = 12,8 cm .s-1
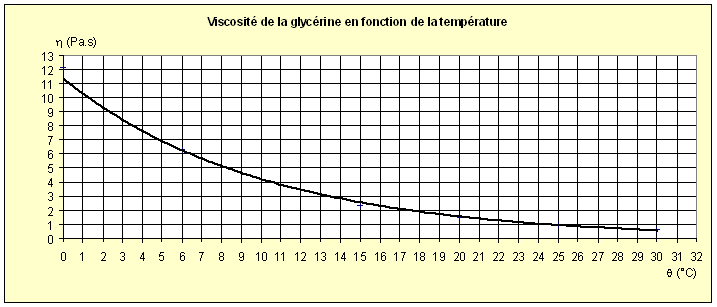
La mesure de la température de la glycérine ( 20 °C ) permet de retrouver la valeur attendue de la viscosité dynamique 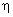 grâce à la courbe ci-dessus : grâce à la courbe ci-dessus :
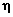 = 1,49 Pa.s . = 1,49 Pa.s .
|
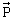 de la bille. (appliqué au centre de gravité G de la bille ; force verticale vers le bas).
de la bille. (appliqué au centre de gravité G de la bille ; force verticale vers le bas). 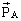 (appliquée au centre de poussée C confondu avec le centre de gravité G de la bille dans le cas étudié) : verticale vers le haut
(appliquée au centre de poussée C confondu avec le centre de gravité G de la bille dans le cas étudié) : verticale vers le haut 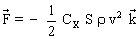 où
où 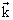 est un vecteur unitaire orienté dans le sens du mouvement de la bille (Force verticale vers le haut).
est un vecteur unitaire orienté dans le sens du mouvement de la bille (Force verticale vers le haut). 

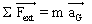 soit
soit 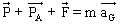
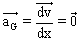 et :
et : 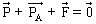
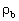 de la bille et de son volume :
de la bille et de son volume : 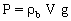 .
. 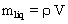 où
où 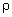 est la masse volumique de la glycérine donc
est la masse volumique de la glycérine donc 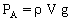 .
. 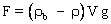
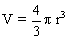 ou encore, puisque r =
ou encore, puisque r = 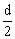 (d : diamètre de la bille),
(d : diamètre de la bille), 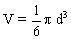 .On a alors :
.On a alors : 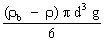
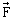 est
est 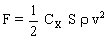 avec
avec 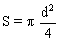 ; L'égalité précédente est réécrite :
; L'égalité précédente est réécrite : 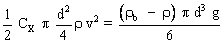
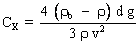 {E}
{E}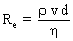 , v correspond à la vitesse moyenne relative du fluide par rapport au solide (dans le cas étudié : la bille supposée sphérique) , d est le diamètre intérieur du tube dans lequel s'écoule le fluide ou le diamètre de la bille en mouvement dans le fluide (dimension « caractéristique » du système étudié).
, v correspond à la vitesse moyenne relative du fluide par rapport au solide (dans le cas étudié : la bille supposée sphérique) , d est le diamètre intérieur du tube dans lequel s'écoule le fluide ou le diamètre de la bille en mouvement dans le fluide (dimension « caractéristique » du système étudié).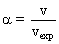 où vexp est la vitesse expérimentale de chute de la bille dans la glycérine (milieu limité par les parois du tube) et v la vitesse qu'aurait cette même bille dans la glycérine si le milieu était infini. C'est cette vitesse v à prendre en compte dans le calcul du nombre de Reynolds.
où vexp est la vitesse expérimentale de chute de la bille dans la glycérine (milieu limité par les parois du tube) et v la vitesse qu'aurait cette même bille dans la glycérine si le milieu était infini. C'est cette vitesse v à prendre en compte dans le calcul du nombre de Reynolds. 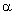 ; La relation utilisée est :
; La relation utilisée est : 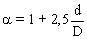

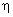 grâce à la courbe ci-dessus :
grâce à la courbe ci-dessus : 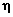 = 1,49 Pa.s .
= 1,49 Pa.s . 