PHYSIQUE Donné en mai 2000
EXERCICE :
On veut maintenir constante la température d'une pièce d'habitation, en hiver. Dans ce problème on étudie les pertes de chaleur à travers le mur. Les échanges thermiques avec les autres pièces de l'habitation seront supposés nuls. On rappelle les lois de transfert de la chaleur, utiles dans le problème :
Conduction : loi de Fourier :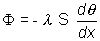 
,
où 
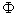est le flux
de chaleur (ou puissance thermique) à travers une surface S , et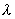 
la
conductivité thermique du matériau traversé.
Convection : loi de Newton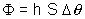 
,
où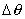 
est l'écart
de température entre la paroi et le fluide et h le coefficient d'échange par
convection entre le fluide et la paroi.
Les échanges de chaleur dans un solide se font par conduction et ceux entre un solide et un fluide se font par convection.
Evaluation des pertes de chaleur :
1. Pour un mur d'épaisseur e, limitée par deux plans parallèles de surface
S maintenus à des températures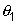 
et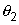 
constantes,
justifier que le flux de chaleur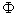
à travers chaque section du mur est constant.
2. En Intégrant la loi de Fourier, établir l'expression du flux de chaleur
en fonction de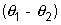 
.
Le matériau constituant le mur est supposé homogène et on notera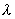
sa conductivité thermique.
3. Exprimer les flux de chaleur échangés par convection au niveau des surfaces intérieures et extérieures du mur. On notera h le coefficient d'échange air-solide par convection.
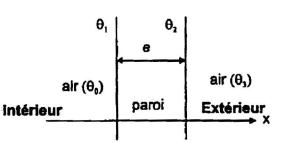
Justifier l’ égalité de ces trois flux. En déduire que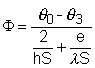 
4. Le mur extérieur d'une pièce d'habitation a 2,70 m de hauteur, 4,10m de
longueur et 25 cm d'épaisseur. Il est constitué de briques de conductivité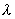
= 0,665 W.m -1.K-1.
Au centre du mur est située une fenêtre de dimensions 1,50 m x 1,60 m. Les
vitres ont une épaisseur de 5 mm et une conductivité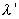 
= 0,778 W.m -1.K-1
On admet que le coefficient d'échange air-solide est le même à l'intérieur et à l'extérieur, on prendra h = 11,4 W.m -2.K-1.
Sachant que la température extérieure est de 0°C et la température intérieure de 19°C, calculer le flux de chaleur :
- à travers les briques
- à travers les vitres.
En déduire le flux total F à travers le mur.
5. Calculer la déperdition d’ énergie horaire à travers le mur.
|
|
|
|
|
|
|
